1. 误区：只看收益率高低

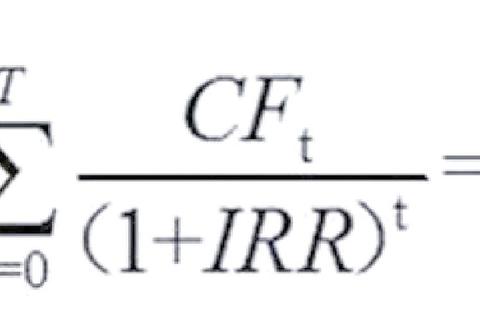
很多人在评估投资时，习惯性比较"年化收益率"或"总回报率"，却忽略了资金的时间价值。例如：有人对比两个项目，A项目3年总回报50%，B项目5年总回报80%，便直接认定B项目更优。实际上，如果考虑资金回笼速度，用IRR（内部收益率）计算会发现，A项目的年化收益率可能高达14.5%，而B项目仅有12.4%。

更典型的误区是手动计算IRR时，误把简单除法当公式。比如初始投资10万，三年后收回15万，有人直接用（15-10）/10/3=16.6%作为年化收益。但按IRR公式计算实际只有14.5%，误差源自未考虑每年现金流差异。

2. 技巧一：理解现金流时间轴

案例：教育金规划

张女士计划为儿子准备大学学费，当前投入5万元，未来4年每年追加2万，第5年取出18万元。看似总投入13万，收回18万，表面收益率38%。但用IRR计算：

现金流序列：-50000, -20000, -20000, -20000, -20000, +180000

通过Excel的IRR函数计算，实际年化收益率仅为6.7%。这是因为早期持续投入压制了资金增值效率，必须用时间轴精确计算每笔现金流的现值。

3. 技巧二：活用Excel工具计算

操作指南：

1. 在A1-A6单元格依次输入：-100000,30000,40000,50000,60000,70000（初始投资10万，后续5年回报）

2. 在空白单元格输入公式：=IRR(A1:A6)

3. 按回车显示12.3%，即该项目的真实收益率

进阶场景处理：

当现金流日期不固定时（如私募基金季度分红），需使用XIRR函数。例如某基金投资记录：

2023/1/1 投入50万

2023/6/30 分红3万

2024/12/31 收回58万

公式=XIRR(B1:B3,A1:A3)可计算出精确的年化收益率9.8%。

4. 技巧三：结合NPV交叉验证

案例对比：

两个投资项目初始均需100万：

虽然IRR相同，但计算净现值（NPV）时会发现差异。假设折现率10%：

项目甲NPV=200/(1+10%)^5 -100=24.6万

项目乙NPV=170/(1+10%)^3 -100=27.3万

这说明IRR相同情况下，资金回收更快的项目实际价值更高，需结合NPV做决策。

5. 答案：IRR的正确使用法则

通过实证分析，我们得出三条铁律：

1. 时间加权原则：2023年回收1万元比2025年回收1万元价值高13%（按10%折现率）

2. 工具辅助原则：复杂现金流必须使用XIRR计算，手工计算误差可达5%-15%

3. 多维评估原则：某房地产项目IRR达22%，但若考虑空置期现金流中断，实际IRR会降至17%

最终建议投资者建立动态评估模型：先用IRR筛选收益率>12%的项目，再用NPV比较具体价值，最后结合回收期控制风险。例如某组合投资，IRR13.2%且85%本金能在前两年收回，就是优质选择。